4.2. De binomiale verdeling
Als je 100 zuivere dobbelstenen gooit, hoeveel vieren vallen er dan? We proberen het drie keer achter elkaar:
rbinom (1, size=100, prob=1/6)## [1] 20rbinom (1, size=100, prob=1/6)## [1] 20rbinom (1, size=100, prob=1/6)## [1] 23Of 50 keer achter elkaar:
rbinom (50, size=100, prob=1/6)## [1] 25 17 16 16 17 19 16 14 16 16 25 12 17 14 10 22 14 18 16 13 12 15 14
## [24] 14 20 20 12 14 11 19 15 20 25 16 18 14 14 18 24 19 19 18 23 16 11 17
## [47] 19 17 20 13Of 100 miljoen keer achter elkaar:
a = rbinom (1e8, size=100, prob=1/6)
hist (a, breaks=40)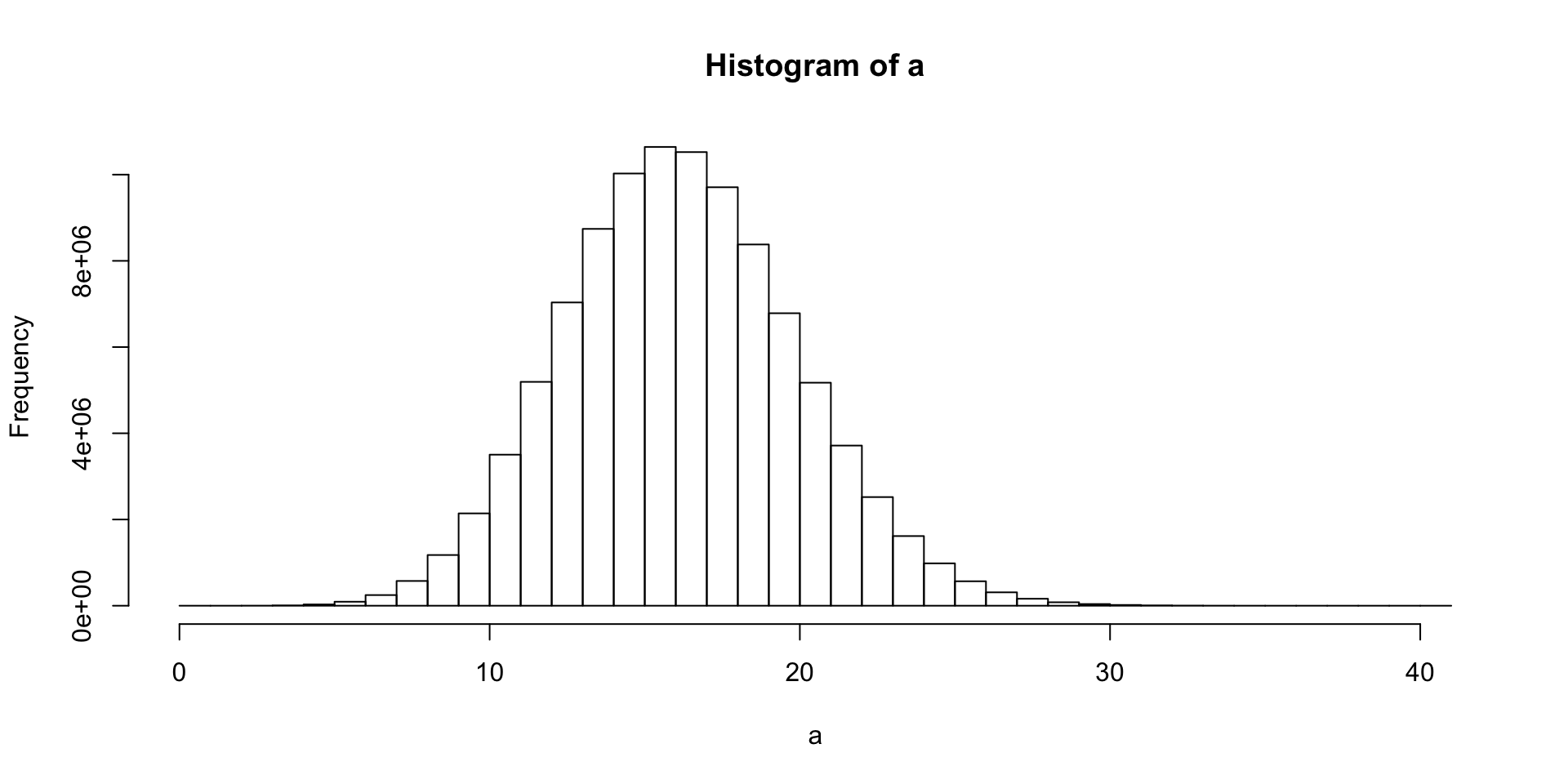
De modus ligt bij 16 en 17; geen wonder, dat is 1/6 van 100. De staart naar rechts is net een beetje langer dan die naar links; geen wonder, want het minimum aantal keren kop is 0 en het maximum is 100.
De theoretische verdeling kan ook getekend:
curve (dbinom (x, size=100, prob=1/6), from=0, to=40, n=41)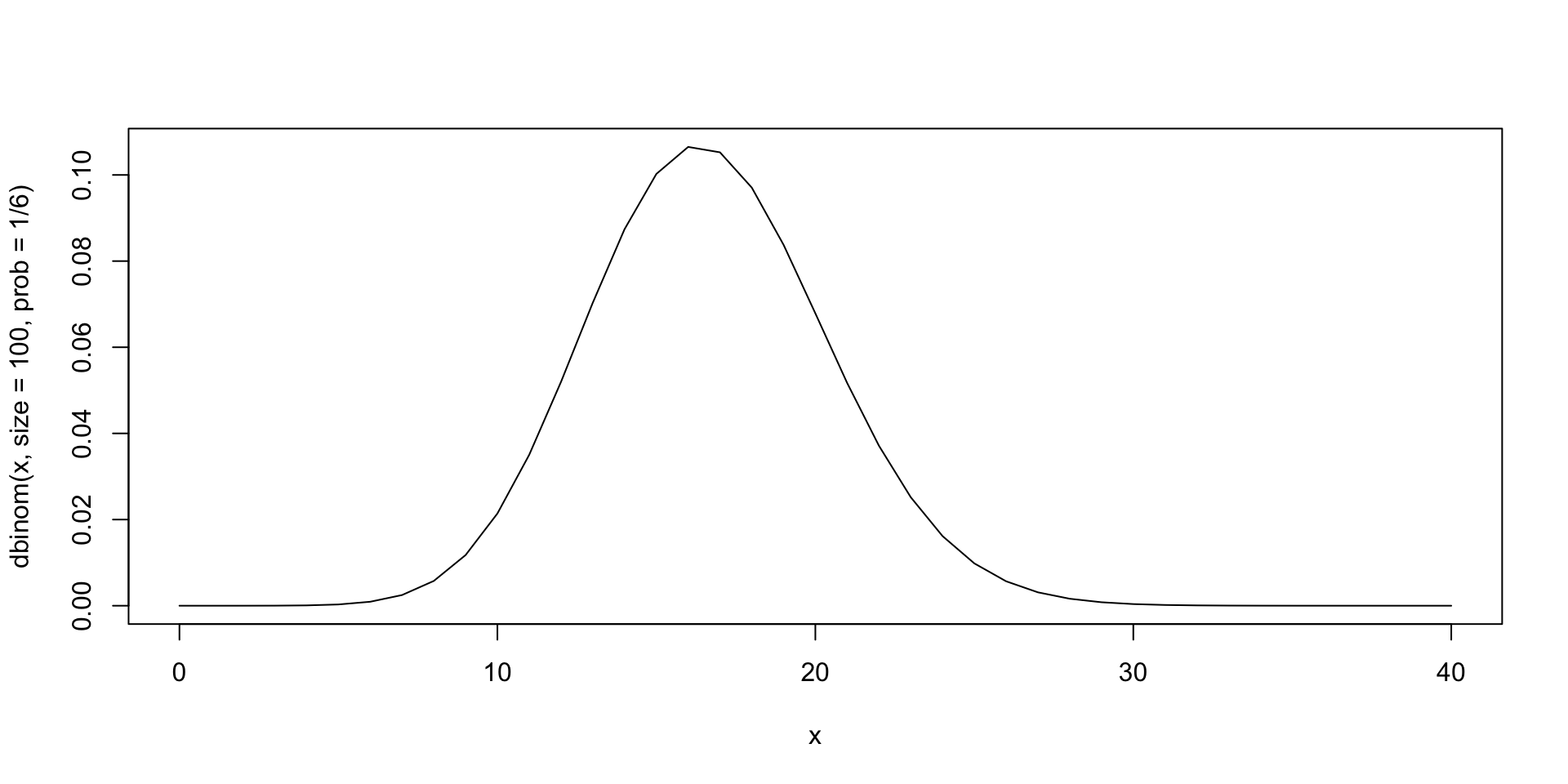
Deze grafiek is hoekig, omdat de punten alleen voor de gehele getallen getekend zijn. De functie dbinom geeft namelijk de kans dat een bepaald aantal vieren valt (bij dnorm was dat de kansdichtheid). Dus bv. de kans dat er 16, 17, 18, 24 of 25 vieren vallen is:
dbinom (16, size=100, prob=1/6)## [1] 0.1065014dbinom (17, size=100, prob=1/6)## [1] 0.1052485dbinom (18, size=100, prob=1/6)## [1] 0.09706247dbinom (24, size=100, prob=1/6)## [1] 0.01616099dbinom (25, size=100, prob=1/6)## [1] 0.009825882De kans dat er hoogstens 16, 17, 18, 24 of 25 vieren vallen is:
pbinom (16, size=100, prob=1/6)## [1] 0.494159pbinom (17, size=100, prob=1/6)## [1] 0.5994074pbinom (18, size=100, prob=1/6)## [1] 0.6964699pbinom (24, size=100, prob=1/6)## [1] 0.9782966pbinom (25, size=100, prob=1/6)## [1] 0.9881225Zoals je ziet kloppen dbinom en pbinom met elkaar:
pbinom (25,size=100,prob=1/6) - pbinom (24,size=100,prob=1/6)## [1] 0.009825882De kans dat er meer dan 24 (dus 25 of meer) vieren vallen is
1 - pbinom (24, size=100, prob=1/6)## [1] 0.02170338of ook
pbinom (24, size=100, prob=1/6, lower=F)## [1] 0.02170338Onder welk aantal vieren hebben we maar 2.5% van de uitkomsten? En boven welk aantal vieren?
qbinom (0.025, size=100, prob=1/6)## [1] 10qbinom (0.975, size=100, prob=1/6)## [1] 24Tenslotte: als we 24 vieren aantreffen in onze 100 worpen, en we nemen niet aan dat de dobbelsteen zuiver is, wat zijn dan de met de observatie compatibele kansen op een vier?
binom.test (24, n=100)##
## Exact binomial test
##
## data: 24 and 100
## number of successes = 24, number of trials = 100, p-value =
## 1.81e-07
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.1602246 0.3357355
## sample estimates:
## probability of success
## 0.24Dus de observatie van 24 vieren uit 100 worpen is compatibel met alle ware kansen op een vier die liggen tussen 16.0% en 33.6%.