6.1. Lineaire regressie met één continue factor
Lineaire regressie zul je meestal uitvoeren op experimentele data waarvan je niet precies weet wat het onderliggende model is. In dit hoofdstukje geef ik echter een voorbeeld van data waar het onderliggende model wel bekend is, om vervolgens te kijken hoe gaat de lineaire regressie dat onderliggende model kan vinden.
Voorbeeld van een lineair model: schoenmaat als lineaire functie van de leeftijd. We weten dat voeten groeien tussen dat je 0 en 18 jaar oud bent. Stel dat we ook weten dat in de populatie van Nederlandse pasgeborenen de gemiddelde schoenmaat 17.9 is, en dat de schoenmaat per jaar met 1.2 toeneemt. Dus in de populatie van Nederlandse kinderen die hun eerste verjaardag vieren, is de gemiddelde schoenmaat 19.1, op de tweede verjaardag is de gemiddelde schoenmaat 20.3, en op de 18de verjaardag is de gemiddelde schoenmaat \(18+1.2\times 18=39.5\). Zo’n constante toename heet een lineaire toename, omdat je hem kunt weergeven als een lijn:
curve (17.9 + 1.2 * x, xlim = c(0,18))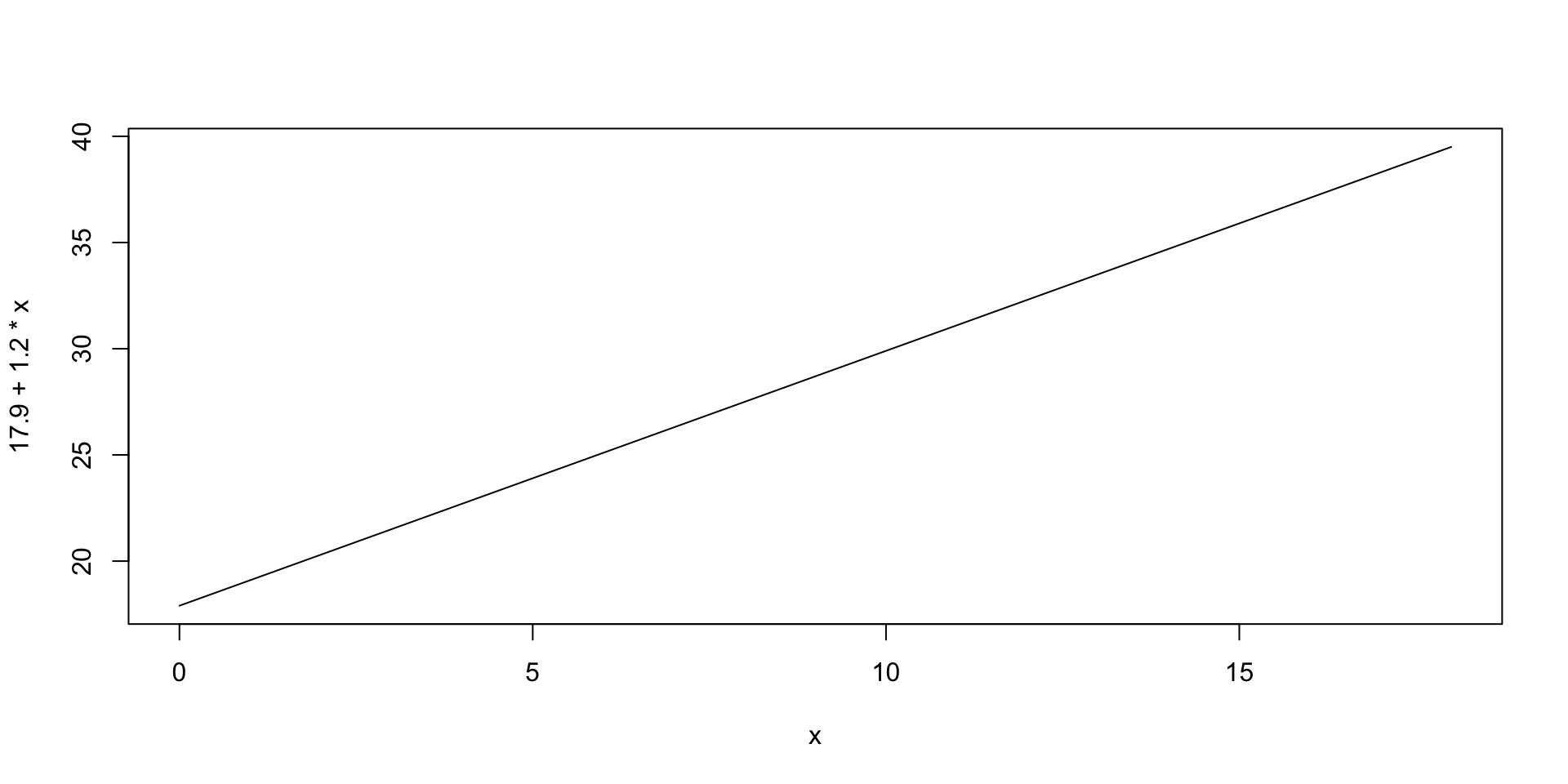
Deze lijn snijdt de y-as (de verticale lijn waar \(x=0\)) bij \(y=17.9\), en daarom heet 17.9 de intercept van de lijn. Het getal 1.2 heet de helling van de lijn. De volgende wiskundige vergelijking drukt deze lijn uit: \[ gemiddelde\ schoenmaat = 17.9 + 1.2 \times leeftijd \] Je werkelijke schoenmaat zal van meer dingen afhangen dan de leeftijd alleen, zoals van je genen, of van je voeding, of van wat niet al. Als de standaardafwijking van de schoenmaten op elke leeftijd 2.0 is, d.w.z. de standaardafwijking van de schoenmaten binnen de populatie van 1.6-jarigen is 2.0, en de standaardafwijking van de schoenmaten binnen de populatie van net 15.3-jarigen is ook 2.0, enzovoort, dan is het lineaire model als volgt: \[ schoenmaat = 17.9 + 1.2 \times leeftijd + {\cal N} (0, 2.0) \]
Gesimuleerde data. We trekken eerst een aselecte steekproef van 100 mensen uit de populatie van 0- tot 18-jarigen. Als alle leeftijden in de populatie even vaak voorkomen, zijn leeftijden uniform verdeeld. De 100 mensen hebben dan de volgende leeftijden:
leeftijden = runif (100, min = 0.0, max = 18.0)
leeftijden## [1] 9.06725696 13.75199849 1.23169247 16.33399555 16.54516048
## [6] 2.65922064 17.35747014 11.03443279 9.16624663 2.59636517
## [11] 8.25528689 7.63172396 14.15615472 4.61977861 17.76068814
## [16] 8.03475260 9.65015395 4.10200604 4.02661334 9.08341931
## [21] 8.85071618 12.19542926 0.07047901 8.85524892 14.09766891
## [26] 0.98989478 16.25179078 7.27399499 17.46309829 10.58835496
## [31] 3.78130385 10.91882298 10.82526499 6.02494238 17.09834328
## [36] 17.25797179 1.65059979 9.71650955 12.96243307 4.68697208
## [41] 13.84258453 16.98071407 1.57850738 14.93445464 17.38172545
## [46] 12.32748707 6.01154782 13.99721368 11.64144634 7.14504124
## [51] 16.04133556 9.28857124 3.34759526 9.20639660 11.72717493
## [56] 8.58356781 14.87716764 10.59071784 10.42888970 12.46533368
## [61] 16.04353719 13.21257901 1.96901098 15.39793850 6.89753742
## [66] 7.21381407 7.04306768 9.73568882 9.07241784 2.45686046
## [71] 10.78885240 17.89086243 5.43885153 11.32070306 14.40803400
## [76] 17.21062189 4.24095390 9.34189151 11.34881770 4.60034938
## [81] 3.51087237 9.75571780 6.03631205 1.01254607 3.07049045
## [86] 1.39197883 13.42010589 14.43913995 9.57802921 2.31583524
## [91] 14.58974088 8.77207348 11.79472837 13.46948672 6.46604106
## [96] 11.31956193 0.07471847 12.58177433 9.87699333 7.29618220Deze leeftijden zijn niet afgerond op gehele getallen. Tenslotte groei je het hele jaar door door.
De schoenmaten van deze 100 mensen zijn:
schoenmaten = 17.9 + 1.2 * leeftijden + rnorm (100, sd = 2.0)
schoenmaten## [1] 30.34084 37.66571 20.90565 38.08400 37.54917 21.77079 39.94710
## [8] 30.24552 28.31304 21.02948 27.99620 28.13734 33.88429 26.17807
## [15] 36.59388 26.97208 34.91962 26.72294 22.51828 31.61801 26.09534
## [22] 35.66987 13.35871 26.20023 33.54273 17.74878 38.58845 23.51794
## [29] 39.12800 28.30344 24.69719 30.46835 30.15603 24.17170 41.06095
## [36] 36.49526 20.95360 27.42472 34.95576 25.36399 30.46152 40.29212
## [43] 18.40131 36.55530 35.66145 28.68431 22.99396 32.23869 34.60196
## [50] 25.91328 34.12542 27.74072 22.33791 28.06966 32.07703 26.18222
## [57] 35.20144 27.56529 32.47159 33.07049 37.01399 32.76300 20.46921
## [64] 36.95528 28.02657 25.97285 24.01966 30.28730 31.49062 22.67045
## [71] 28.81146 41.29594 25.13579 29.63590 38.00249 41.68286 20.09523
## [78] 31.84822 28.92174 20.53791 22.22619 27.14189 25.88265 20.30097
## [85] 19.14394 16.94523 36.15115 34.41225 31.32523 23.13025 33.60332
## [92] 29.08134 35.21664 35.43749 25.93802 33.83018 18.11393 32.29376
## [99] 29.25761 26.60845Als losse getallen zijn deze data niet goed te begrijpen, maar als scatterplot wel:
plot (leeftijden, schoenmaten, xlim = c(0, 18))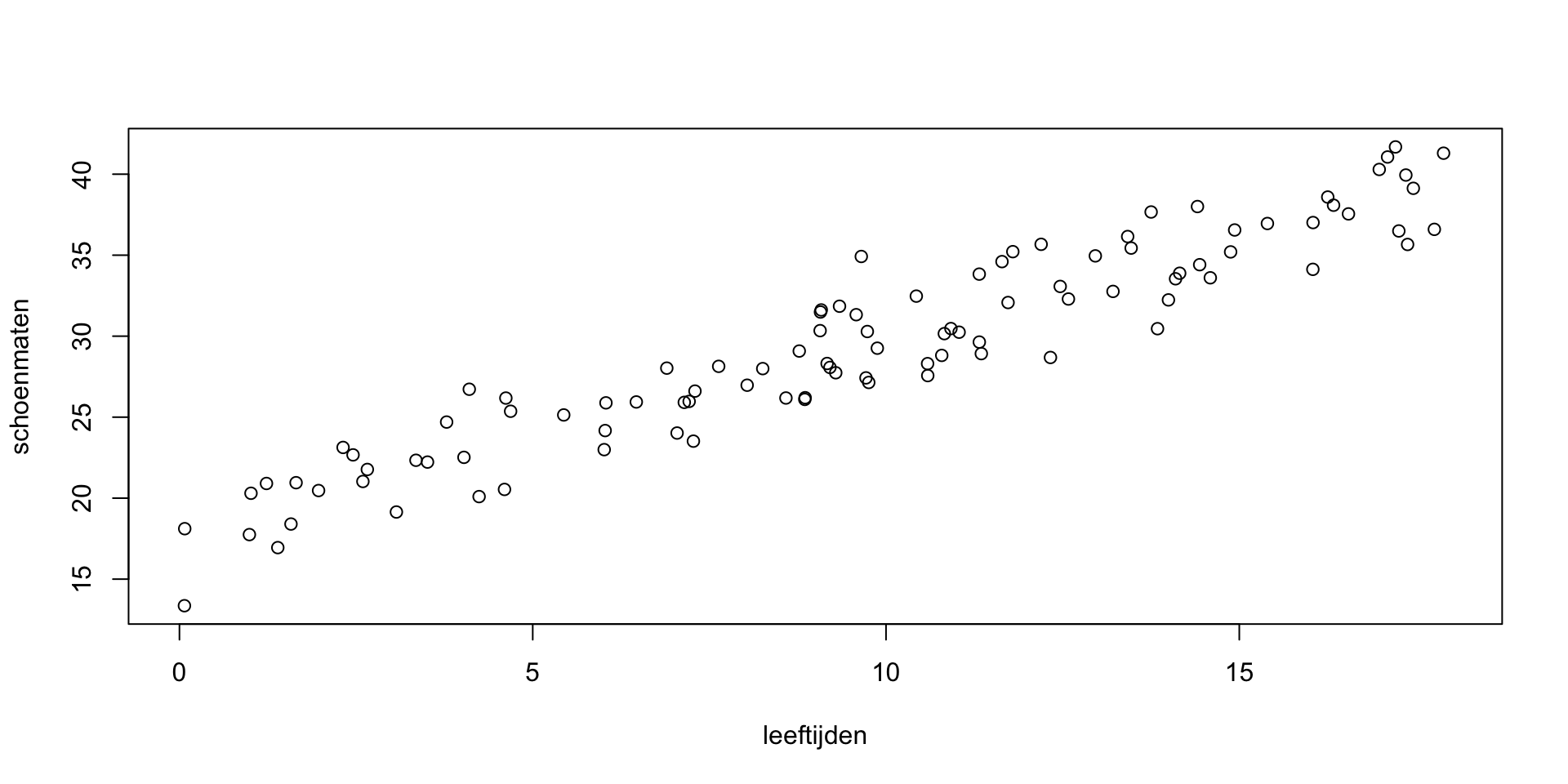
Zo te zien liggen de data wel ongeveer op één lijn.
De lineaire regressie. Uit een echt experiment kun je data krijgen die er zo uitzien als de scatterplot hierboven. Aan de lineaire regressie de opdracht om een lijn midden door die data te trekken (“fitten”). Omdat we stiekem weten dat de data gegenereerd waren met een intercept van 17.9 en een helling van 1.2, hopen we dat de intercept en helling van de lijn die de lineaire regressie voor ons gaat vinden, ongeveer 17.9 respectievelijk 1.2 zijn.
Het model dat door de lineaire regressie gemaakt wordt, is een lijn: \[ y=\beta_0+\beta_1 x+\epsilon \] waarbij \(\epsilon\) een normaal verdeeld toevalsgetal is (de “error”) met gemiddelde 0 en standaarddeviatie \(\sigma\). We weten stiekem dat \(\beta_0=17.9\), \(\beta_1=1.2\), en \(\sigma=2.0\), maar de lineaire regressie weet dat nog niet.
De 100 punten die we hebben, voldoen aan de formule \[
y_i=\beta_0+\beta_1 x_i+\epsilon_i
\] voor \(i=1..100\). In de werkelijkheid van het onderzoek hebben we echter alleen de beschikking over de 100 punten (\(x_i\), \(y_i\)), en zouden we graag een schatting willen maken van \(\beta_0\), \(\beta_1\) en \(\sigma\). Deze schattingen noemen we \(b_0\), \(b_1\) en \(s\) (van Grieks naar Latijn dus). Met andere woorden, we zoeken zodanige waarden voor \(b_0\), \(b_1\) en \(s\) dat de volgende formule zo goed mogelijk klopt: \[
y_i≈b_0+b_1 x_i
\] Om precies te zijn: we zoeken \(b_0\), \(b_1\) en \(e_i\) (\(i=1..100\)) in \[
y_i=b_0+b_1 x_i+e_i
\] zodanig dat het gemiddelde van alle \(e_i\) nul is, en de som van hun kwadraten zo klein mogelijk. Dat kan met de hand, maar gelukkig heeft R er een snelle berekening voor (lm betekent “linear model”):
lm (schoenmaten ~ leeftijden)##
## Call:
## lm(formula = schoenmaten ~ leeftijden)
##
## Coefficients:
## (Intercept) leeftijden
## 17.766 1.211De formule met de tilde, dus schoenmaten ~ leeftijden, spreek je uit als “schoenmaten als functie van leeftijden”. De coëfficiënt \(\beta_0\) (de intercept) wordt dus geschat op \(b_0=17.7657977\), en de coëfficiënt \(\beta_1\) (de helling) wordt geschat op \(b_1=1.2105744\). Deze waarden komen aardig overeen met de onderliggende 17.9 en 1.2.
De lijn kunnen we in de grafiek tekenen:
plot (leeftijden, schoenmaten)
abline (b0, b1) # als je dit nadoet, wel even de juiste b0 en b1 invullen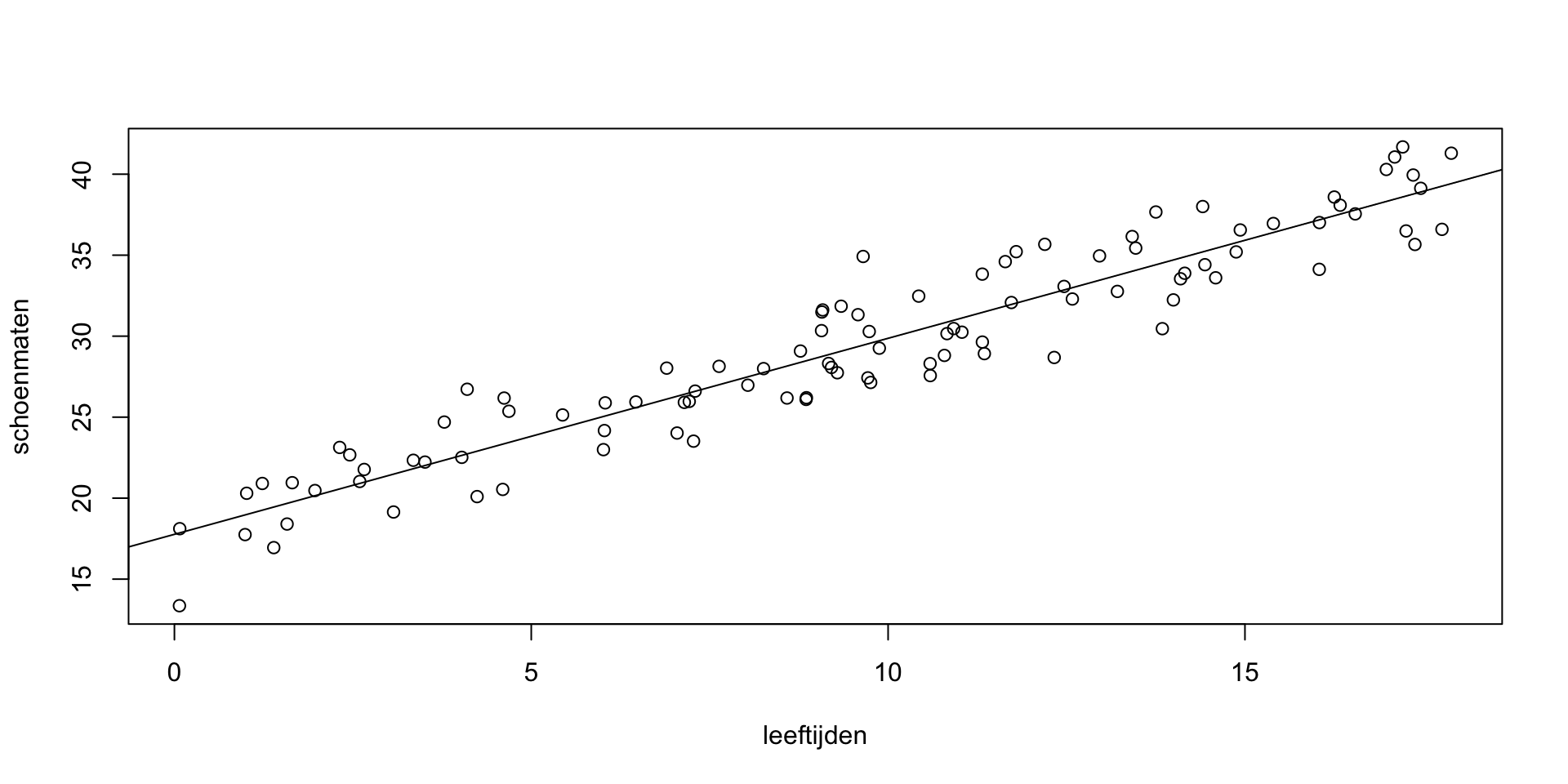
Cruciale informatie. De vorige paragraaf gaf te weinig informatie: alleen de schattingen van de parameters van het model. Meestal willen we ten minste ook nog weten of die schattingen significant verschillen van 0. Daarvoor is het commando summary, dat gek genoeg meer informatie geeft dan wanneer je het model zelf print:
model = lm (schoenmaten ~ leeftijden)
summary (model)##
## Call:
## lm(formula = schoenmaten ~ leeftijden)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.4924 -1.8269 0.1176 1.6110 5.4716
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 17.76580 0.45091 39.4 <2e-16 ***
## leeftijden 1.21057 0.04188 28.9 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.062 on 98 degrees of freedom
## Multiple R-squared: 0.895, Adjusted R-squared: 0.8939
## F-statistic: 835.5 on 1 and 98 DF, p-value: < 2.2e-16De “residuen” waarover hier gesproken wordt, zijn de 100 getallen \(e_i\). Hun bereik en drie quartielen worden genoemd (waarom niet het gemiddelde?). De “residual standard error” is een beetje een rare term, maar geeft een schatting van \(\sigma\); het is dus de bovengenoemde \(s\). Komt aardig in de buurt van de ware waarde van \(\sigma\), die 2.0 is. De p-waardes geven de significantie van \(b_0\) en \(b_1\) vergeleken met 0 aan. Dat die 17.7657977 significant verschilt van 0 zegt dat pasgeborenen gemiddeld een schoenmaat hebben die groter is dan 0, en dat die 1.2105744 significant verschilt van 0 zegt dat de schoenmaat gemiddeld toeneemt met de leeftijd.
Betrouwbaarheidsintervallen. Het geven van een p-waarde tegen 0 is wel het minimum aan informatie dat je rapporteren moet als je een parameter van een lineaire regressie rapporteert, maar de meeste tijdschriften moedigen je echt aan om vooral ook de betrouwbaarheidsintervallen van de parameters te geven. Bijvoorbeeld: de boven gevonden waarde van de helling (1.2105744) is slechts een puntschatting (point estimate) van de helling, maar het betrouwbaarheidsinterval geeft je alle waarden van de helling waarmee je data compatibel zijn:
confint (model)## 2.5 % 97.5 %
## (Intercept) 16.870976 18.660619
## leeftijden 1.127461 1.293688Het betrouwbaarheidsinterval voor de helling loopt van 1.127461 tot 1.2936878. Omdat in 95% van de gevallen (als we dit experiment vaak uitproberen met nieuwe steekproeven en telkens opnieuw een betrouwbaarheidsinterval uitrekenen) de berekende betrouwbaarheidsintervallen de werkelijke helling bevatten, kan een rationele gokker 19 tegen 1 (d.w.z. 95 tegen 5) gokken dat de ware helling tussen 1.127461 en 1.2936878 ligt. In zekere zin (met Bayes gesproken) hebben we op grond van de data 95% kans dat de ware intercept tussen 1.127461 en 1.2936878 ligt; frequentisten houden er niet van om dit zo te zeggen, omdat de ware intercept (die, hoewel onbekend voor iemand die alleen de data ziet, 1.2 is) nu eenmaal ofwel tussen 1.127461 en 1.2936878 ligt (met kans 1) of wel buiten dat interval ligt (ook met kans 1). In ieder geval kun je zeggen dat een gokker op grond van de data 95% zeker kan zijn dat tussen 1.127461 en 1.2936878 de ware helling ligt.
Verder is het zo dat bij alle nulhypotheses (voor de helling) tussen 1.127461 en 1.2936878 de aangetroffen geschatte helling van 1.2105744 een p-waarde heeft die groter is dan 0.05 (deze relatie tussen p-waarde en betrouwbaarheidsinterval geldt voor alle gaussische modellen); daaruit volgt dat zeggen dat de geschatte helling van 1.2105744 significant van 0 verschilt gelijkwaardig is aan zeggen dat 0 buiten het betrouwbaarheidsinterval van de helling valt. Deze gelijkwaardigheid zagen we ook al bij de t-toets.