Bruce Schneier has developed a methodology called "attack trees" for analyzing and designing security. These are described in Chapter 21 of his new book, _Secrets and Lies_, and also the Dr. Dobbs article on attack trees. This author has invented a methodology, for using attack trees to analyze the controls needed to implement trusted services.
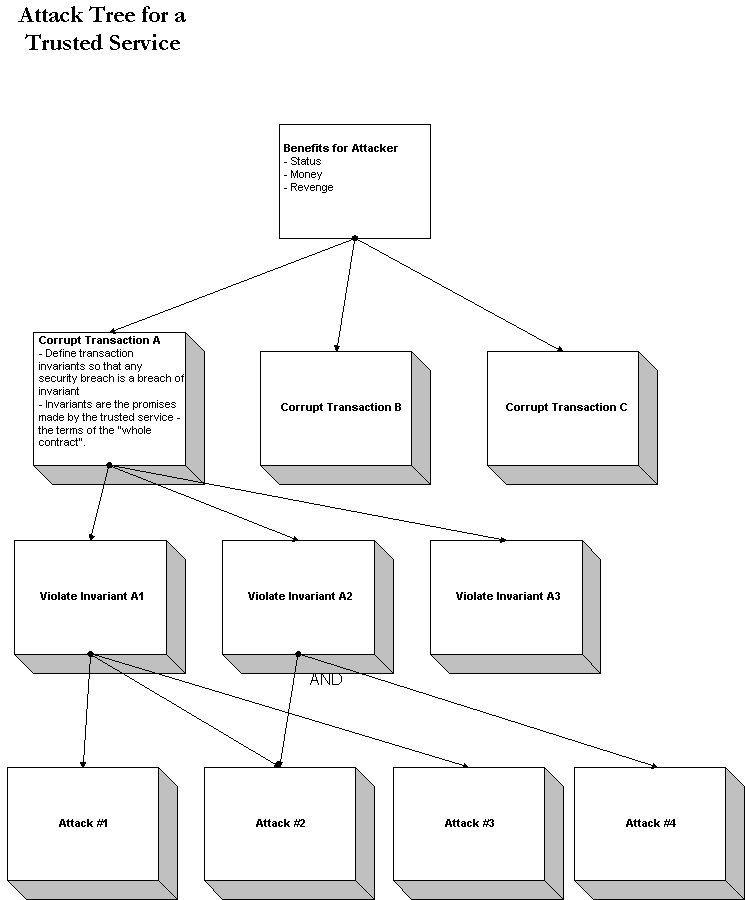
We describe a trusted service as a series of transactions -- say A, B, and C. These transactions have desired invariant properties. For example transaction A has desired properties A1, A2, and A3. This means that when the transaction is completed (this might be a temporal logic "eventually" or might have a strict deadline) the transaction should be in states such that statements A1, A2, and A3 are true. For example, a desired invariant property could be "the goods have been shipped if and only if the payment has been made".
Violating these desired invariants are then treated as the goals of the attacker. We proceed to build an attack tree for each invariant. This tree technically is a directed acyclic graph, since a particular security breach (e.g. attacker opening a safe) may be a useful step in violating more than one of the transaction invariants.
One can define a trusted third party service in terms of what it promises to do, or what customers reasonably expect it to do, and then construct an attack tree as per above.
Most attacks against trusted services come from insiders, not
outsiders. Business has evolved over the centuries a rich tradition
of structures for securing transactions from their own employees.
These structures prevent or deter theft or fraud by requiring
cooperation to fulfill or change a transaction. When these
structures are successful, employees cannot individually commit
fraud but must at least collude or compromise the security
of the other to do so.
"Group controls" is my term that encompasses a variety of these constraints and checks placed on the individual members of an organization. The term "group controls" is most closely related to, and encompasses, the term "internal controls" in auditing, but also encompasses the checks created by third party records (e.g. shippers and payment services), by external audits, and by the security technologies that facilitate the creation of group controls.
These structures allow trusted organizations such as banks, brokerages, and so on to be achieve a trustworthiness greater than the trustworthiness of any particular employee. Indeed, for a global business particular employees are usually strangers to customers, so customers have no good reason to trust them.
Alas, there is little theory showing how these structures work - auditors adapt this rich tradition ad hoc. As we radically transform our institutions from paper media to digital, we need to develop ways of designing provable group control structures rather than merely carrying on traditions that, while highly evolved, may now often be obsolete.
This author has invented a methodology for examing and designing group control structures in terms of attack trees. Here for example is the design of a dual control structure:
(0) Construct an attack tree. Attacker goals include compromise of any of the important properties of the transaction the organization is trusted to perform. Focus on the _internal_ threats. Any place where an employee has access to or responsibility for a security step, examine what happens if the employee _is_ the attacker.
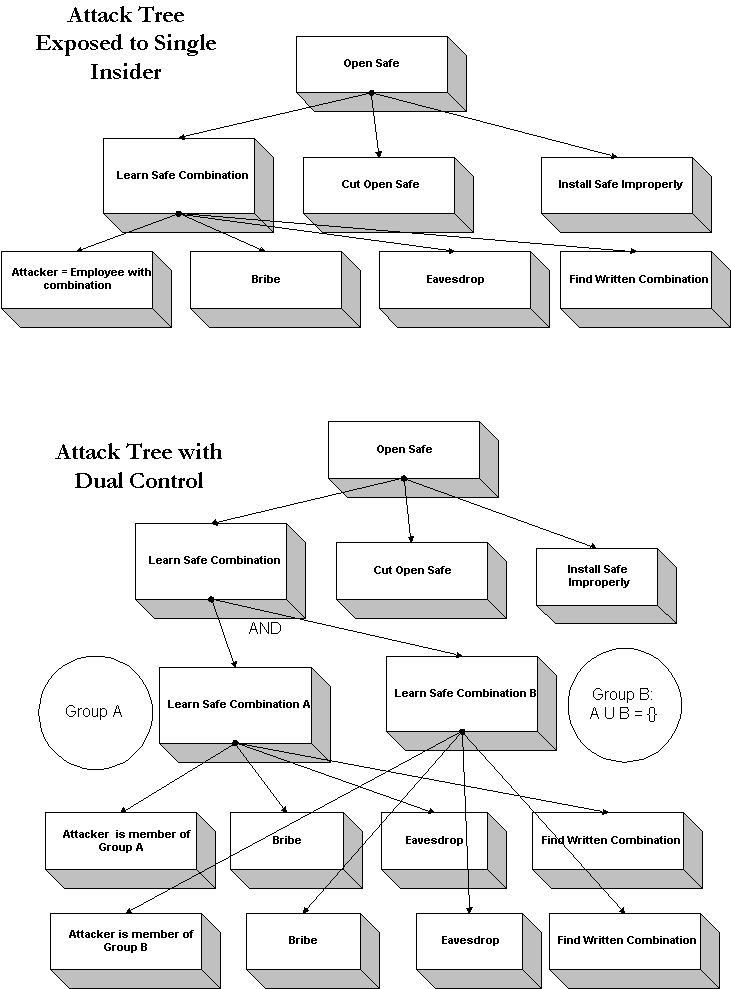
(1) Start with single node in an OR structure on an attack tree. (It doesn't have to be a leaf node -- in fact the more leaf attacks are encompassed by the node, the better). This node should represent a weakness in the security, especially nodes that involve trusting single employees. Let's use Bruce's example of the attack tree for opening a safe. We add a new subnode to the "Learn Combination" node -- "Employee trusted with combination = Attacker". Now the attacker can trivially achieve his goal!
(2) For this node create a security layer that requires two independent participants to achieve the (sub)goal of the node. Instead of just a single combination in the "Learn Combination" mode we set up the safe to require two different combinations.
(3) Give the two independent access means to two disjoint groups. For example group A learns combination A and group B learns combination B. The groups should only be large enough to provide sufficient reliability - if somebody in group A is absent there are other people in group A to take over the function. Any pair of members, one from each group, can cooperate to process a transaction according to the rules defining a trustworthy transaction, or the pair may choose to collude to violate those rules.
(4) This creates an AND node where there was previously a single node. Instead of a single insider being able to break the security at that node, a member from group A AND a member from group B must collude to achieve the attacker's goal at that node. Subnodes A and B each inherit (usually independent) copies of the subnodes of the former node.
In Bruce's safe example, the attacker must threaten, blackmail, eavesdrop, bribe, or be (via collusion) _both_ A and B. The attacker can mix and match -- the attacker could be a member of A and eavesdrop on a member of B, say when Bob of B is carelessly inputting the combination without shielding the view.
Note that not only does our dual control address the "Employee = Attacker" node we added; the dual control also strengthens security against the other subnodes of "Learn Combination". This will be the case when the attacker must now attack each group indepdenently. In the safe combination the independence is great but not complete -- Alice eavesdropping on careless Bob shows that there is still some vulnerability from having members of A and B operate in close proximity.
The above methodology can easily be extended to triple control control structures and more esoteric separations of duties.
Secure logging and review by a party from a third group C, for example, add a further AND subnode. Adding these to the above described dual control, we get a group control structure where a member from group A must collude with or compromise the security of a member from group B AND the reviewer from group C must fail to detect or respond to the collusion.
Schneier attack trees allow these structures and collusion probabilities to be examined in terms of the overall attack threat. Group control structures allow us to design trustworthy services and to communicate to customers why these services, conducted by individuals who are total strangers to the customers, can nevertheless be trusted.
